
20 Episódios da História da Matemática
Dos primeiros artefatos à invenção do Cálculo
Frederico Andries Lopes
Direitos autorais © 2020 Frederico Andries Lopes
Dados Internacionais de Catalogação na Publicação (CIP)
(Câmara Brasileira do Livro, SP, Brasil)
_______________________________________________________
Lopes, Frederico Andries
20 episódios da história da matemática [livroeletrônico] : dos primeiros artefatos à invenção do cálculo /
Frederico Andries Lopes. -- 1. ed. -- Palmas, TO : Frederico Lopes, 2020.
ISBN 978-65-00-13182-6
1. Matemática - Estudo e ensino I. Título.
20-50214 CDD-510.7
_______________________________________________________
Índices para catálogo sistemático:1. Matemática : Estudo e ensino 510.7
Aline Graziele Benitez - Bibliotecária - CRB-1/3129
Capa: Frederico J. A. Lopes
Revisão: Maria Perla Araújo Morais
As imagens desta obra foram ou criadas pelo autor ou estão disponibilizadas sob a licença Creative Commons.
Nenhuma parte deste livro pode ser reproduzida ou armazenada em um sistema de recuperação ou transmitida de qualquer forma ou por qualquer meio, seja este eletrônico, mecânico, fotocópia, gravação ou outro sem a permissão expressa por escrito do autor.
Impresso no Brasil.
Dedicado aos meus pais,
os professores
Alcione e Henderson
Sumário
Eratóstenes, seu crivo e a circunferência da Terra
Hipácia e o fim da tradição matemática grega
Omar Kayyam, a poesia e a matemática
Cardano, a álgebra e a probabilidade
Bombelli e os números complexos
Descartes e a geometria analítica
Introdução
Este livro surgiu de 20 pequenos textos que elaborei como parte do material usado em um curso de História e Filosofia de Matemática oferecido pela Universidade Federal de Mato Grosso (UFMT), em 2020, na modalidade à distância. Escritos para alunos e alunas que teriam um primeiro contato com a história da matemática, esses textos foram inicialmente publicados em meu site pessoal, fredlopes.com.br , e ainda lá se encontram, em uma versão ligeiramente diferente da que apresento aqui.
Além de servir de material para um curso formal, minha segunda intenção ao escrevê-los foi proporcionar a um público mais amplo uma introdução agradável a uma área de pesquisa fascinante sob muitos aspectos. No fim de cada capítulo, acrescentei, para divertir os leitores, uma seção de discussão com provocações sobre matemática, filosofia e educação que nem sempre se encontram na bibliografia “oficial” sobre o tema.
Também na página dedicada à história da matemática do meu site estão alguns artigos de interesse histórico que traduzi diretamente das línguas originais, principalmente o latim e o francês. Essas fontes primárias podem ser lidas paralelamente a alguns dos capítulos deste livro, fornecendo uma aura de concretude à matemática, que passa a ser vivenciada através dos artigos fundadores da própria disciplina.
Gostaria de agradecer aqui à equipe com quem trabalhei na formatação e no emprego deste material nos cursos em que ele foi utilizado, professores e professoras ligados à Universidade Aberta do Brasil da UFMT, em especial ao prof. Dr. Sérgio Antonio Wielewski. Outro agradecimento necessário vai para a profa. Dra. Maria Perla Morais que, além de ter feito a revisão desta produção, contribuiu com muitas sugestões ao texto final.
E que o leitor ou a leitora guarde bem no coração o seguinte: as muitas horas de pesquisa e escrita deste livro, em que procurei equilibrar precisão e segurança de informações com um texto agradável, foram para mim fontes de muita alegria. Espero que, na leitura deste livro, você possa sentir o mesmo!
O osso de Ishango

O osso de Ishango é um dos mais antigos artefatos “matemáticos” conhecidos. Encontrado em 1960 pelo geólogo belga Jean de Heinzelin (1920-1998) na localidade de Ishango, na atual República Democrática do Congo, esse pequeno osso de babuíno contém três conjuntos de marcas distintas, feitas por algum material cortante com intenções ainda hoje desconhecidas.
Segundo datações recentes, o osso teria entre 18.000 e 22.000 anos de idade, cerca de 10.000 anos mais antigo do que o início da agricultura e dos primeiros núcleos humanos permanentes conhecidos. Como ocorre com todo artefato arqueológico, uma série de especulações é imediatamente criada para dar algum sentido ao objeto encontrado. Partindo de uma visão moderna, nossa primeira interpretação é dizer que o autor das marcas estava “contando” alguma coisa. Mas há quem extrapole essa simples versão e diga muito mais.
A figura anterior não nos deixa ver com precisão que há três colunas de marcas feitas ao redor do osso, como as colunas de uma tabela. A seguir, temos uma visão esquemática dessas marcas, como se tivéssemos “desenrolado” o osso:

Observe algumas características dessas marcas:
Na coluna à esquerda, as marcas se dividem em pequenos grupos de 11, 13, 17 e 19 marcas, e somam 60.
Na coluna do meio, encontramos conjunto de 3, 6, 4, 8, 10, 5, 5 e 7 marcas, e somam 48.
Na coluna à direita, vemos 11, 21, 19 e 9 marcas, e somam 60.
Um observador moderno, além de perceber que a soma das marcas de cada coluna é divisível por 12, poderia observar também:
A coluna da esquerda tem todos os números primos entre 10 e 20
A coluna central tem o padrão “um número e seu dobro”, como 3 e depois 6, 4 e depois 8, 10 e suas metades 5 e 5, e por fim o número 7 fora desse padrão
A coluna da direita apresenta números ao redor de alguma de dezena, como 10 + 1, 20 + 1, 20 - 1 e 10 – 1, e todos são ímpares
Seriam essas características suficientes para dizer que a pessoa que fez as marcas estava desenvolvendo algum tipo de pensamento matemático? Ou será que, segundo algumas interpretações, ela estaria contando os ciclos da lua? Se a pessoa que fez as marcas era mulher, estaria ela contando fases de seu ciclo menstrual? Não sabemos. Nenhuma dessas interpretações encontrou guarida definitiva entre arqueólogos e antropólogos, mas é muito forte a percepção de que essas marcas representariam a contagem de alguma coisa.
Existem ossos mais antigos do que esses, como o osso de Lebombo (c. 37.000 a.C.), mas nenhum com características tão marcantes. Até que outros artefatos com a mesma estrutura sejam encontrados, não poderemos dizer, com certeza, do que o osso de Ishango trata.
Discussão
O problema central da história da matemática é um problema de historiografia , de escrita da história. Como escrever a história da matemática? O que conta como matemática e o que não conta? Quais fatos são relevantes? Seria o osso de Ishango um fato da história da matemática? Afinal, o que é mesmo matemática para que possamos classificar e historiar todo o material?
Diante disso, o osso de Ishango desperta alguns questionamentos para você refletir:
Riscos e entalhes em qualquer objeto, se feitos com algum padrão, contam como matemática? Não seriam, talvez, apenas arte?
Seria possível que a pessoa que fez os entalhes no osso estivesse apenas passando tempo? A existência de marcas que vemos como possuindo alguma estrutura que nós chamamos de matemática pode ser obra de uma pessoa que estivesse apenas se divertindo?
Você acredita que a pessoa que entalhou o osso tinha palavras para expressar quantidades?
Plimpton 322

Em 1922, um editor de Nova York de nome George Plimpton comprou de um comerciante displicente, por apenas 10 dólares, uma pequena tabuinha de argila com marcas feitas com algum tipo de estilete. Plimpton viu algum valor histórico na peça, mas não soube precisar do que se tratava, e acabou doando a tabuinha à Universidade de Columbia. Foi então que os pesquisadores descobriram um dos mais fascinantes documentos da história da matemática na antiguidade.
A Plimpton 322 faz parte de uma ampla coleção de documentos escritos em argila da antiga civilização mesopotâmica, que floresceu entre os rios Tigre e Eufrates, na região onde hoje se encontra o Iraque. Datada de 1.800 a.C., a Plimpton 322 nos dá um diminuto vislumbre do que foi a matemática mesopotâmica e do grau elevado dos conhecimentos dos povos daquela região. Deles herdamos muitos conhecimentos, mas principalmente a divisão da circunferência em 360 partes e da hora em 60 minutos.
Mas os matemáticos e astrônomos mesopotâmicos sabiam muito mais. A Plimpton 322 é uma lista de ternos pitagóricos , uma sequência de três números que satisfazem o teorema de Pitágoras, como 3, 4 e 5, que formam os lados de um triângulo retângulo. As três primeiras colunas contêm os ternos, em notação sexagesimal , e a quarta apresenta apenas os números de 1 a 15, o que mostra que os ternos estavam sendo sistematicamente coletados.
Como sempre, as interpretações sobre o artefato variam. A tabela poderia ter sido escrito para uma aula elementar de álgebra ou de trigonometria ou mesmo como um simples exercício de escrita cuneiform e por algum escriba aprendiz. De qualquer maneira, ficamos com a impressão de que aquela tabela não era utilitária, ou seja, suspeitamos que a civilização que a produziu tinha preocupações com o conhecimento desinteressado, desligado de alguma aplicação prática imediata, e com o desenvolvimento de técnicas matemáticas por seu próprio valor intelectual.
Como esses números foram gerados? Os matemáticos da Mesopotâmia conheciam as fórmulas que produziam os ternos pitagóricos ou a Plimpton 322 é uma mera compilação de ternos descobertos empiricamente? A tendência é aceitar a primeira hipótese, mas, até que nossos estudos sejam realizados e novas descobertas sejam feitas, a questão permanece aberta.
Discussão
O que podemos aprender com a Plimpton 322? Esse número, 322, ligado ao nome Plimpton, nos indica que essa é apenas uma de uma longa série de tabuinhas de argila. Há 321 antes e existem centenas depois. A civilização mesopotâmica, criadora de muitos dos mitos que ainda habitam nosso imaginário, conhecidos através dos hebreus que escreveram a Bíblia, certamente legaram muita ciência ao nosso mundo moderno. Algumas reflexões são possíveis:
Uma vez criado um sistema numérico suficientemente complexo, será que ele adquire “vida própria”, sendo cultivado pelo seu valor intrínseco, além de necessidades puramente materiais?
Como seria uma aula de matemática naquele tempo? Estariam esses conhecimentos destinados a figurar apenas nos escritos de uma casta de intelectuais e cientistas ou eram também acessíveis a mais pessoas através de um processo de educação sistemática?
O papiro de Rhind

Por volta de 1.650 a.C., um certo escriba egípcio chamado Ahmes (ou Amósis) finalizou aquela que seria não a mais antiga, mas a mais notável obra de matemática egípcia de que temos conhecimento: um livro escrito sobre uma imensa folha de 5,5 metros por 30 cm de altura, feita com tiras prensadas do caule de uma planta chamada papiro. Finalizada a escrita, essa longa folha era, então, enrolada e transportada como se fosse um bastão, e passava, assim, a ser catalogada em grandes bibliotecas de papiros. Mas o que dizia esse livro em particular que tanto interessa a matemáticos e historiadores da ciência?
Esse notável papiro foi comprado em 1858 pelo advogado e egiptologista Alexander Rhind, em uma visita que fazia à cidade de Luxor. Adquirida em 1864 pelo Museu Britânico, a obra foi batizada de papiro de Rhind, e continua fascinando arqueólogos e historiadores.
Do que trata o papiro de Rhind? O pequeno trecho do papiro, que vemos na imagem acima, nos mostra que há triângulos e o que parecem ser as medidas dos lados. Há um retângulo, um trapézio e o que se assemelham a tabelas de números empilhados. Existe, apenas nesse pequeno trecho, muita coisa parecida com aquilo que chamamos de matemática. E o que mais tem o papiro?
O papiro contém dezenas de problemas de aritmética, frações, cálculo de áreas, volumes, progressões, repartições proporcionais, regra de três simples, equações lineares, trigonometria básica e geometria. É coisa suficiente para nos fazer imaginar uma longa tradição cultural transmitida e ampliada de geração a geração. Uma dessas tradições culturais, talvez a mais antiga de todas as tradições científicas, seja a da transmissão de conteúdos de matemática através de problemas ficcionais, desligados de qualquer consideração prática. Um dos problemas que o papiro discute em detalhes é o seguinte:
Sete casas contêm sete gatos. Cada gato mata sete ratos. Cada rato comeu sete espigas de grãos. Cada espiga de grãos teria produzido sete hekats (medidas) de trigo. Qual é o total de tudo isso?
Esse é um problema interessante, o início de uma tradição que persiste até hoje. Em particular, a do uso do número 7 em problemas parecidos que vêm aparecendo de maneira persistente em várias tradições científicas do mundo todo. Você saberia resolvê-lo?
O papiro tem outras interessantes características. É o mais antigo exemplar da história que contém símbolos para as operações matemáticas. Por exemplo, o sinal de mais era denotado por um par de pernas andando em direção ao número a ser adicionado (você consegue ver alguns na figura acima?). Isso nos mostra que a matemática é também uma linguagem que necessita de seu próprio código, sua própria notação, para além da notação da língua falada. Mas por que isso ocorre?
Discussão
Estudiosos não têm dúvidas de que o papiro de Rhind era uma cópia feita por Ahmes de outros papiros mais antigos. Ahmes fazia parte de uma escola de escribas, cujo treinamento consistia em copiar dezenas e dezenas de papiros em escrita hierática como parte de sua educação. Tudo isso nos leva a crer que as ciências matemáticas egípcias eram mais extensas e mais antigas do que o papiro de Rhind nos deixa antever.
Baseados no que vimos, o que podemos pensar das seguintes questões:
Platão afirmava que a geometria teve início no Egito, a partir da experiência de medir áreas de plantações. No entanto, a construção das pirâmides exigiu muito mais do que o simples cálculo de áreas. Para que, afinal, você imagina que serviam os conhecimentos matemáticos dos egípcios?
Por que os egípcios transmitiam seus conhecimentos matemáticos preferencialmente através de problemas recreativos?
Egípcios eram muito bons em lidar com frações, principalmente com frações unitárias, aquelas que têm numerador igual a 1. Você seria capaz de expressar o número 0,575 como soma de 3 frações unitárias que tenham denominador menor do que 10?
Pitágoras e os pitagóricos

O teorema de Pitágoras é, sem dúvida, o mais conhecido teorema de toda a geometria, ensinado em todas as escolas e utilizado extensamente em toda a matemática. A pessoa à qual é atribuído, o filósofo grego Pitágoras de Samos (c. 570 – c. 495 a.C.), no entanto, é bem menos conhecida.
Figura semilendária do século VI a.C., Pitágoras foi o líder de uma seita que acreditava, entre muitas outras coisas, que os números – puros, livres e incorruptíveis – eram alguma coisa próxima de entidades divinas, possuidoras de consciência e de influência direta na vida prática dos homens. Pitágoras e seus discípulos, conhecidos como pitagóricos, estão também entre os primeiros cientistas a exigir argumentos racionais para diversos fatos matemáticos conhecidos como teoremas. Eles deram início, juntamente a Tales de Mileto (c. 624 – 546 a. C.), considerado o primeiro filósofo ocidental, à forma de matemática dedutiva que hoje estudamos nas universidades.
A mais famosa demonstração do teorema de Pitágoras aparece nos Elementos , de Euclides de Alexandria (fl. c. 300 a.C.). A demonstração, no entanto, não é de Pitágoras, mas do próprio Euclides. Pitágoras não demonstrou com toda generalidade o teorema que leva o seu nome, mas apenas percebeu sua validade em casos particulares. Também não foi seu descobridor: os matemáticos mesopotâmicos conheciam as ternas pitagóricas, como vimos, e quase certamente conheciam sua expressão geométrica, assim como os egípcios, também excelentes geômetras.
Não se conhece nada que Pitágoras tenha escrito. Uma longa tradição lhe atribui muitos feitos, muitas descobertas, mas as primeiras obras escritas sobre sua vida só apareceram cerca de… 800 anos depois de sua morte! Em outras palavras, quase tudo o que se sabe dele e de sua fraternidade é fruto de transmissão oral, um telefone sem fio bastante persistente, mas nada confiável. Platão (428 – 348 a.C.), o grande pai da filosofia ocidental, foi profundamente influenciado pela tradição pitagórica. E daí, pela influência de Platão, temos o pitagorismo ainda evidente em nossa cultura.
Segundo a tradição – ao falarmos de Pitágoras, estaremos sempre nos referindo a essa tradição –, Pitágoras e seus discípulos não foram simples místicos em busca de um ritual, mas também cientistas sagazes. Eles observaram, por exemplo, que cordas vibrantes tocadas juntas produziam sons harmoniosos, agradáveis ao ouvido, se seus tamanhos mantivessem razões expressas por inteiros, preferencialmente pequenos, como 1/2, 2/3 e 3/4. A teoria musical que ainda hoje estudamos teve início com essas simples observações.
Os pitagóricos estudaram também propriedades dos números figurados, como os números triangulares, retangulares e pentagonais, sugerindo diversas relações entre eles. Descobriram os números perfeitos, aqueles que são a soma de seus divisores próprios, como o 6 (divisores próprios: 1, 2 e 3, e daí 6 = 1 + 2 + 3) e 28 (divisores próprios: 1, 2, 4, 7 e 14, e daí 28 = 1 + 2 + 4 + 7 + 14).
Essa sanha aritmética levou Pitágoras a afirmar que “tudo é número”, um dogma religioso rapidamente refutado pela famosa crise dos incomensuráveis. De maneira simplificada, essa crise se originou com a descoberta de que números como a raiz quadrada de 2 ou de 5 não podem ser expressos como uma razão (divisão) entre dois números inteiros. No fim do choque criado por essa descoberta, a sociedade pitagórica não existiria mais, mas sua poderosa influência criativa pode ser sentida ainda hoje em diversos campos das artes, da filosofia e das ciências.
Discussão
Os pitagóricos estão no fundamento e no coração de muito do que veio a ser conhecido como filosofia ocidental. Sua história continua a inspirar místicos e cientistas, admirados com a candente originalidade de suas contribuições. E, como tudo na história, os pitagóricos levantam diversas questões:
Juntamente a Tales de Mileto, Pitágoras e seus discípulos introduziram na matemática os primeiros exemplos de argumentos puramente racionais conhecidos como demonstrações. Os povos mesopotâmicos e egípcios não chegaram a conhecer tais instrumentos intelectuais. Será, então, que a ideia de demonstração deveria ser ensinada nas escolas, uma vez que muito da matemática utilitária de que necessitamos sobrevive sem ela?
Em sua opinião, existe alguma relação necessária entre matemática e misticismo, ou isso é apenas uma característica particular dos pitagóricos?
A numerologia que vemos em livros e sites da internet, promovendo poderes extraordinários de certos números, é uma descendente contemporânea do misticismo aritmético pitagórico. Você consegue imaginar algum argumento concreto que a justifique?
Euclides e seus Elementos

Euclides (fl. c. 300 a.C.) foi um importante matemático grego que viveu em Alexandria, no Egito. É considerado popularmente como o “pai da geometria”, ainda que esse epíteto esteja errado em cada palavra.
Pouco se sabe sobre sua vida, exceto que desenvolveu sua obra sob o reinado de Ptolomeu I do Egito (323 – 283 a.C.). Mais do que geometria elementar, Euclides escreveu sobre a teoria dos espelhos, ótica e astronomia esférica. Mas é pela sua obra máxima, chamada de Elementos , que ele se imortalizou, exercendo a mais duradoura influência no pensamento humano jamais alcançada por outro cientista.
Euclides é melhor denominado como o sistematizador do método axiomático, a maneira de ordenar o conhecimento baseado em axiomas e teoremas. O método axiomático, que funciona muito bem na matemática, consiste em fundamentar todos os fatos sobre determinados objetos em cima de uma diminuta base de afirmações primitivas conhecidas como axiomas. A partir dos axiomas, novas afirmações são derivadas – os teoremas – por um poderoso motor intelectual cujas peças são as regras da lógica. Foi através desse método que Euclides ordenou em treze livros boa parte do conhecimento matemático elementar de sua época.
Os Elementos , traduzidos pela primeira vez diretamente do grego por Irineu Bicudo, e publicado no Brasil pela Editora da Unesp em 2009, está dividido em 13 livros:
O livro 1 contém 23 definições, 5 postulados e 9 noções comuns, e cobre tópicos importantes da geometria plana, como o teorema de Pitágoras, igualdade de ângulos e áreas, paralelismo, soma dos ângulos de um triângulo e a construção de várias figuras geométricas;
O livro 2 contém vários lemas (teoremas preparatórios para outros teoremas) relativos à igualdade de retângulos e quadrados, às vezes chamados de “álgebra geométrica”, e conclui com uma construção da proporção áurea e uma maneira de construir um quadrado com área igual a qualquer figura plana;
O livro 3 trata de círculos e suas propriedades. Mostra como encontrar seu centro, trata de ângulos inscritos, tangentes, potência de pontos e o teorema de Tales;
O livro 4 constrói o incírculo e o circuncírculo de um triângulo, assim como mostra a construção de polígonos regulares com 4, 5, 6 e 15 lados;
O livro 5, o primeiro dos chamados livros aritméticos, trata de proporções de magnitudes e apresenta a teoria altamente sofisticada da proporção, provavelmente desenvolvida por Eudoxo de Cnido (408 a.C – 355 a.C);
O livro 6 aplica a teoria das proporções à geometria plana, especialmente na construção e no reconhecimento de figuras semelhantes;
O livro 7 trata da teoria dos números elementares: divisibilidade, números primos e sua relação com números compostos, o algoritmo de Euclides para encontrar o maior divisor comum e como encontrar o mínimo múltiplo comum;
O livro 8 trata da construção de sequências geométricas de números inteiros;
O livro 9 aplica os resultados dos dois livros anteriores, prova a infinidade de números primos e apresenta a construção de todos os números perfeitos pares;
O livro 10 prova a irracionalidade das raízes quadradas de números inteiros não quadrados, como a raiz de 2, e classifica as raízes quadradas de segmentos incomensuráveis em treze categorias distintas. Euclides apresenta o termo irracional, com um significado diferente do conceito moderno de número irracional. Ele também fornece uma fórmula para produzir ternas pitagóricas;
O livro 11 generaliza os resultados do livro 6 para figuras sólidas: perpendicularidade, paralelismo, volumes e semelhança de paralelepípedos;
O livro 12 estuda os volumes de cones, pirâmides e cilindros usando o método da exaustão, um precursor da integração, e mostra, por exemplo, que o volume de um cone é um terço do volume do cilindro correspondente. Conclui mostrando que o volume de uma esfera é proporcional ao cubo de seu raio (na linguagem moderna), aproximando seu volume por uma união de muitas pirâmides;
O livro 13, por fim, constrói os cinco sólidos platônicos regulares inscritos em uma esfera e compara as proporções de suas arestas com o raio da esfera.
Boa parte desses conteúdos são contribuições de matemáticos anteriores. A Euclides são reputados diversos resultados originais e muitas demonstrações, inclusive a belíssima demonstração do teorema de Pitágoras. Mas como foram ordenados todos esses conhecimentos?
Euclides começa o livro 1 com uma série de 23 definições controversas, como “ponto é aquilo de que nada é parte”, “linha é comprimento sem largura” e outras 21 definições. Logo depois, enuncia os 5 seguintes postulados, que modernamente chamamos de axiomas:
Fique postulado traçar uma reta a partir de todo ponto até todo ponto.
Também prolongar uma reta limitada, continuamente, sobre uma reta.
E, com todo centro e distância, descrever um círculo.
E serem iguais entre si todos os ângulos retos.
E, caso uma reta, caindo sobre duas retas, faça ângulos interiores e do mesmo lado menores do que dois retos, sendo prolongadas as duas retas, ilimitadamente, encontrarem-se no lado no qual estão os menores do que dois retos.
Dos postulados acima, o quinto é o mais estranho e também o mais importante. Não tem a aparência de uma afirmação elementar, e nos faz suspeitar que seja um teorema deduzido dos postulados anteriores. De fato, foi isso o que matemáticos de todas as épocas tentaram: mostrar como deduzir o quinto postulado dos quatro anteriores. Esses esforços redundaram em geniais fracassos, mas ocasionaram o desenvolvimento das geometrias não-euclidianas, geradas quando o quinto postulado é substituído por outros. As geometrias não-euclidianas, longe de serem filhas de especulações desinteressadas de matemáticos puros, são usadas hoje em muitas áreas da tecnologia, principalmente na teoria da relatividade de Albert Einstein (1879 – 1955), que, entre outras coisas, garante o bom funcionamento do sistema de GPS em todo o planeta.
Após esses postulados, Euclides apresenta as noções comuns , nove axiomas supostamente aplicáveis a todos os ramos do conhecimento, como, por exemplo, “o todo é maior do que a parte” e “os dobros da mesma coisa são iguais entre si”. Sobre essa base de definições, postulados e noções comuns, centenas e centenas de teoremas são demonstrados, em um encadeamento lógico que encanta e convence.
Os Elementos tratam de matemática elementar, mas sua leitura não é nada fácil. A tradução de Irineu Bicudo, a primeira feita diretamente do grego, é tão idiossincrática, por assim dizer, que podemos considerá-la uma obra destinada a eruditos: só é recomendada para quem deseja aprender o grego de Euclides comparando-o com o português de Bicudo. Mas foi essa mesma a intenção do tradutor: estabelecer um padrão ouro para a tradução de textos da antiguidade grega. Esperamos que, futuramente, uma boa alma retraduza os Elementos tornando-o palatável a um público mais geral. Enquanto isso não ocorre, vamos refletir mais um pouco sobre algumas questões pertinentes aos Elementos e seu uso científico.
Discussão
A importância dos Elementos é impossível de ser avaliada, de tão extensa e profunda. Muitas questões são ainda hoje levantadas, mas as seguintes podem servir de ponto de partida para o educador matemático:
O método axiomático é uma das grandes conquistas da ciência ocidental. Sua aplicação em áreas diversas da matemática chegou a produzir intuições profundas sobre uma espantosa quantidade de assuntos. No entanto, ainda que persista na matemática, ele está bastante desgastado em outras disciplinas. Por que não seria esse o método ideal, por exemplo, para ordenar nossos conhecimentos médicos?
A história do ensino de matemática é a história de um longo fracasso. Será que isso é devido à falta de uma organização escolar mais estrita de seus conteúdos, uma que favoreça as ligações internas e profundas entre eles?
Observe a lista de conteúdos dos treze livros. Quais deles você acha que deveriam ser ensinados no ensino básico? Por quê?
Pi
Com as possíveis exceções do 0 (zero) e do 1 (um), nenhum outro número é mais conhecido na matemática do que a constante π. Também nenhuma outra tem uma história tão fascinante.
Seu valor é aproximadamente 3,1415926. Sua história é bem remota e deve ter começado em situações cotidianas. É possível, por exemplo, que povos antigos tenham observado que uma volta da roda de carroça faz a carroça avançar mais ou menos três vezes o valor do diâmetro da roda. É assim que π passa a ser definido, como o número de vezes que devemos multiplicar a medida do diâmetro para encontrarmos a medida da circunferência. Matemáticos gostam de uma definição equivalente: π é a razão entre a circunferência e o diâmetro de um círculo.
Matemáticos egípcios e mesopotâmicos conheciam bem o π. No papiro de Rhind, π tem o valor aproximado de 3,16045, enquanto os matemáticos da Mesopotâmia usavam o valor 3,125. Depois que estudiosos perceberam sua importância em praticamente todos os campos da matemática, a busca pelo seu valor exato deu início a uma das mais longas tradições científicas, o cálculo preciso de suas casas decimais. A luta continua firme e forte: em 29 de janeiro de 2020, Timothy Mullican alegou ter batido o recorde mundial, com o cálculo de 50 trilhões (!) de casas decimais.
π é um
número irracional
. Não pode ser escrito como a razão (divisão) de dois números inteiros. Embora a fração 22/7 dê π com uma boa precisão (3,142857, com as casas decimais se repetindo indefinidamente), sabemos que não existe uma fração que gere todos os seus dígitos, ainda que frações sempre mais próximas possam ser encontradas. π também é um
número transcendente,
ou seja, não é a raiz de nenhuma equação polinomial com coeficientes inteiros, como, por exemplo,
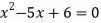 . Isso coloca π em uma categoria especial de números estranhos e interessantes.
. Isso coloca π em uma categoria especial de números estranhos e interessantes.
π é uma letra grega, o que nos faz supor que foram os gregos os primeiros a utilizá-la para batizar a constante 3,1415926…. Mas esse é um engano comum: foi o matemático galês William Jones (1675 – 1749) que a nomeou assim, em um artigo de 1706. Por que π? Porque essa é letra que tem o som de p na língua grega, e a primeira letra da palavra periferia . A história dos símbolos e da notação matemática é tema pitoresco que teremos a oportunidade de abordar ainda outras vezes.
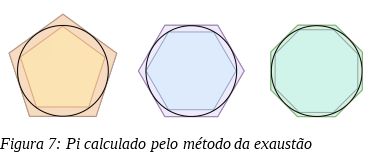
Agora olhe para a figura no início deste capítulo. A primeira figura, mais à esquerda, nos mostra uma circunferência na qual está inscrito um pentágono regular e circunscrito outro. Conseguimos calcular o perímetro do pentágono inscrito sabendo apenas o valor do raio da circunferência, assim como também conseguimos calcular o perímetro do pentágono circunscrito sabendo apenas do valor do raio. Mesmo sem os valores em mãos, podemos conjeturar acertadamente que o perímetro do pentágono inscrito é menor do que o perímetro da circunferência, e também que o perímetro do pentágono circunscrito é maior do que o perímetro da circunferência. Assim, o valor do perímetro da circunferência deve ser algum número entre esses dois valores.
Mas ainda é um valor muito ruim. Se aumentássemos o número de lados dos polígonos regulares inscritos e circunscritos para, por exemplo, como nos mostra a figura, 6 e 8? Não nos parece que esses polígonos estão se transformando, eles mesmos, em uma aproximação da circunferência? Se conseguimos calcular o valor dos perímetros dos polígonos, podemos imaginar que, aumentando o número de lados, conseguiremos aproximar o valor de π com quantas casas decimais quisermos. De fato, esse é o mecanismo básico do chamado método de exaustão , utilizado com sucesso por Arquimedes de Siracusa (c. 287 – c. 212 a.C.) e matemáticos posteriores para solucionar uma infinidade de questões semelhantes. Em particular, esse método era usado para realizar quadraturas , o cálculo de áreas de figuras curvilíneas, o que nos informa que o método da exaustão é um dos precursores da moderna integração.
Madhava de Sangamagrama (c. 1350 – c. 1425), o fundador da Escola de Matemática e Astronomia de Kerala, na Índia, é apenas um das centenas de matemáticos hindus frequentemente ignorados por historiadores. Ainda que tenhamos aprendido a reconhecer a genialidade de matemáticos não-europeus, foi apenas há pouco tempo que reconhecemos uma genial descoberta desse genial indiano, a série de Madhava:
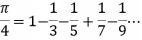
Mas o que essa série tem de especial?
O valor de π sempre foi relacionado a questões geométricas, em especial àquelas envolvendo circunferências. Mas a fórmula de Madhava não faz nenhuma referência a círculos ou figuras curvilíneas. É uma série infinita , um conjunto infinito de números que, se somados, nos dão 1/4 do valor de π. Assim, devemos a Madhava a “libertação” de π de suas humildes origens geométricas para adentrar no mundo da análise matemática, da álgebra e da estatística, aparecendo aqui e ali de maneira fantasmagórica e surpreendente. Alguns séculos depois, essa série foi redescoberta pelo matemático alemão G. W. Leibniz (1646 – 1716). Hoje a série é conhecida por historiadores modernos como série de Madhava-Leibniz, ou apenas como série de Leibniz por matemáticos eurocêntricos empedernidos.
Discussão
Além de importantíssimo, π é divertido e até polêmico. Reflita um pouco mais sobre ele com as questões a seguir:
O cálculo de π é um hobby nerd muito apreciado por programadores de computador e por competidores de campeonatos de memorização, capazes de recitar essa constante com centenas e centenas de casas decimais. Você consegue imaginar algum outro motivo que faz com que cientistas ainda se interessem pelo seu cálculo?
Existe uma certa ansiedade de professores em ensinar as origens e o valor de π. O peso da quantidade descomunal de conteúdos e da exiguidade do tempo e do interesse dos alunos fazem com que a maioria fracasse e acabe estimulando uma decoreba desenfreada de tudo que trate de matemática. Você conseguiria imaginar uma atividade significativa que ensinasse a importância e as origens de π sem apelar para nenhum tipo de memorização?
Alguns matemáticos sugeriram a introdução de uma outra constante, chamada τ (tau), no vocabulário dos matemáticos, valendo duas vezes o valor de π. Assim, entre muitos outros argumentos, a fórmula da circunferência do círculo, C = 2πr se tornaria simplesmente C=τr, revelando melhor a natureza da relação entre a circunferência e o raio do círculo, que é muito mais utilizado do que seu diâmetro. Pesquise um pouco sobre a τ e responda: será que o acréscimo dessa constante no vocabulário matemático resolveria algum tipo de problema de ensino?
Eratóstenes, seu crivo e a circunferência da Terra

Eratóstenes de Cirene (276 a.C. – 194 a.C.), assim como Euclides, foi bibliotecário da famosa Biblioteca de Alexandria, onde escreveu sobre matemática, astronomia, geografia e gramática, além de ter exercido seu estro poético na composição de vários poemas. Veremos aqui duas de suas mais conhecidas contribuições científicas.
A primeira trata da criação de um algoritmo para identificar números primos. Números primos são números divisíveis apenas por 1 e por si mesmos. 17 é um número primo, pois você consegue dividir 17 apenas por 1 e pelo próprio 17. Já 18 não é primo, pois pode ser dividido por 1, 2, 3, 6, 9 e 18. Euclides já havia demonstrado, no livro 9 de seus Elementos , que números primos são infinitos, mas uma questão permanecia: como saber se um dado número é primo?
Eratóstenes teve uma ideia bastante engenhosa para determinar quais números de uma lista de inteiros consecutivos são primos. Para acompanhar o raciocínio, sugiro que você faça o experimento prático: escreva uma lista de números começando de 1 até 100. Você pode escrever quantos números quiser, mas a ideia é apenas entender como o algoritmo funciona. Uma lista inicial de 100 números é suficiente.
Inicialmente, risque o número 1. Agora, faça um círculo no 2, o primeiro primo, e risque da lista todos os múltiplos de 2, como 4, 6, 8, 10, 12 e assim por diante, até o fim da lista, como mostrado na primeira linha da figura do início deste capítulo. Agora faça um círculo no próximo número não riscado , que é o 3, e corte da lista todos seus múltiplos, como 6, 9, 12, 15 e assim por diante, até o fim da lista, como mostrado na segunda linha da figura. Não importa se alguns números já estejam riscados, como os números pares do passo anterior, pois o importante é riscar todos os múltiplos de 3. Agora, observe o próximo número não riscado, que é o 5, e risque todos seus múltiplos, como 10, 15, 20, 25 e assim por diante, até o fim da lista, como mostrado na terceira linha da figura. Repita esse processo até não haver mais números na lista. O que restará serão todos os números primos entre 1 e 100.
O crivo de Eratóstenes foi o primeiro processo sistemático e mecanizado (um algoritmo ) para descobrir números primos. Embora não seja muito bom para lidar com números extremamente grandes, ele deu partida na busca de algoritmos mais eficientes que decidam se um determinado número é primo ou não. Esses esforços estão na raiz de nosso mundo tecnológico: é a extrema dificuldade de se saber se um dado número enorme é primo ou não o que garante a segurança das comunicações na internet. Até que matemáticos descubram um algoritmo para resolver o problema em pouco tempo, você pode se sentir tranquilo em entrar o número de seu cartão de crédito em sites respeitáveis – pelo menos, até um vírus sorrateiro infectar o seu computador!
Outro grande feito de Eratóstenes foi a medição da circunferência da terra, reconhecidamente redonda por filósofos de gerações anteriores. Muito embora esse fato fosse lugar-comum entre os cientistas da época, nenhum deles havia conseguido dizer o quão grande ela era. Coube a Eratóstenes, usando matemática elementar, determinar com bastante precisão sua circunferência.
A história é conhecida. Eratóstenes observou que, ao meio dia de 21 de junho, o sol atinge o ponto mais alto do céu em Alexandria. Observou também que uma estaca fincada no chão produzia uma sombra e que o ângulo entre a estaca e os raios de sol era de 7,2 graus (aproximadamente 1/50 de uma circunferência). Ele sabia também que, em Siena (atual Assuã, no Egito), afastada de Alexandria por cerca de 800 km, a luz do sol não produzia sombras no mesmo dia e à mesma hora, pois era possível vê-lo refletido bem no fundo de um poço. Assim, bastou que ele multiplicasse 50 por 800 para estimar em cerca de 40.000 km a circunferência da Terra. O esquema abaixo pode dar uma ideia do que pensou Eratóstenes.
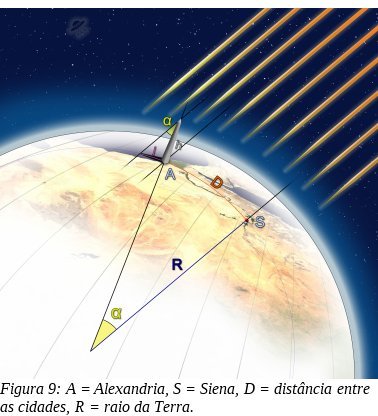
Sabemos hoje que o valor real da circunferência da Terra, se medido ao redor do equador, é de 40.075 km – uma diferença mínima do valor calculado por Eratóstenes.
Discussão
O que podemos aprender com Eratóstenes? As questões a seguir fornecem um bom começo:
Números primos estão no coração da matemática, figurando de maneira central no Teorema Fundamental da Aritmética . Esse teorema afirma que todo número inteiro maior ou igual a 2 pode ser escrito de uma única maneira como um produto de números primos, sem considerar a ordem em que aparecem. Por exemplo, 60 pode ser escrito como 2.2.3.5 e, se ignorarmos a ordem desses números, essa é a única maneira como 60 pode ser escrito como uma multiplicação de números primos. Embora pareça elementar, a importância desse resultado nunca é suficientemente ressaltada. Você conseguiria descobrir por que, afinal, esse teorema é tão importante?
Uma famosa conjetura (um teorema ainda não provado) da matemática, chamada de conjetura de Goldbach , diz que todo número par maior ou igual a 4 pode ser escrito como a soma de, no máximo, dois números primos. Por exemplo, 12 = 5 + 7 e 20 = 7 + 13. Uma excelente maneira de treinar números primos com alunos é fazê-los escrever todos os números pares de 4 a 100 como somas de 2 números primos. Vocês seria capaz de realizar essa tarefa?
Terraplanistas acreditam que a terra não é redonda, apesar de Eratóstenes ter calculado sua circunferência com espantosa precisão há mais de 2.200 anos. Você acredita que a introdução desse tópico nas aulas de ciências ajudaria a reduzir o número de terraplanistas em nossa sociedade?
Diofanto e a álgebra

Isso é grego para mim! Não é assim que falamos quando não entendemos alguma coisa? Agora observe a imagem acima, uma página da Aritmética , de Diofanto de Alexandria (c. 201/215 – 285/299): não só é grego, como também matemática…
Diofanto escreveu sua aritmética por volta do ano 250. É um livro que trata principalmente das soluções em números inteiros de equações com uma ou mais indeterminadas. Um exemplo bem simples seria a equação 3x − 2y = 1, solucionada quando fazemos, digamos, x = 3 e y = 4, uma entre infinitas soluções. Mas as coisas eram um pouco mais avançadas do que esse simples exemplo sugere.
Observe novamente a imagem no início deste capítulo. Onde estão os números e todo aquele conjunto de símbolos a que fomos acostumados na escola? Onde estão as equações? Como aquilo pode ser chamado de matemática? Essas questões apontam para discussões ligeiramente diferentes das que estamos acostumados a ver em livros de história da matemática. Uma busca pela internet nos oferece muitos comentários sobre a Aritmética, de Diofanto, interessantíssima em si mesma, mas tomaremos caminhos laterais para discutir um assunto frequentemente preterido nos manuais técnicos e nos livros didáticos de matemática: a linguagem das ideias matemáticas e de sua cristalização em um conjunto funcional de símbolos.
Não foi Diofanto o primeiro a usar abreviações de palavras ou as próprias palavras como signos com um significado matemático. Os egípcios já faziam isso, e essa tradição estava presente em Alexandria, uma cidade egípcia que se manteve sob o domínio grego por séculos e séculos. Mas o problema é saber por que as palavras comuns do dia a dia não são suficientes para expressar pensamentos matemáticos. Por que todas as culturas, quando tiveram que lidar com conceitos matemáticos, precisaram criar símbolos ou adaptar os já existentes?
Veja a tabela a seguir. Ela mostra a notação moderna e a notação de Diofanto. O que é notável é que não conservamos a notação de Diofanto, assim como não conservamos muitas notações criadas durante a história.

É possível que a notação atual seja substituída por outra mais coerente no futuro. Sabemos que a notação matemática é histórica, ou seja, forjada aos trancos e barrancos para lidar com as ideias e conceitos à medida que são criados. Sabemos também que seus símbolos são polissêmicos, tomando vários significados segundo os contextos em que aparecem. As expressões 3 – 2 e
 contêm os mesmos elementos, mas o traço significa coisas diferentes nas duas. Bastou que os números se posicionassem de forma diferente para o interpretarmos ora como sinal de subtração, ora como de divisão e ora como de razão. Mas o traço em si é o mesmo.
contêm os mesmos elementos, mas o traço significa coisas diferentes nas duas. Bastou que os números se posicionassem de forma diferente para o interpretarmos ora como sinal de subtração, ora como de divisão e ora como de razão. Mas o traço em si é o mesmo.
Além desse problema, a notação matemática parece depender da espacialidade, da possibilidade de escrevermos em todas as direções na folha. Também há problemas com a notação das funções, como a inconsistência do uso do expoente 2 nas expressões cos 2 x e cos x 2 , o que sempre confunde os alunos. Sem dúvida, tradicional não significa melhor.
É possível ver a álgebra simbólica como uma máquina que pode ser manipulada sem que o apelo a um significado seja necessário. A álgebra é o que alimenta a computação moderna, dadas suas regras claras e simples. Por não exigir compreensão, mas apenas manipulação, é a álgebra que acaba figurando como “matemática” na cabeça da maioria dos alunos, que decoram e operam pilhas de regras sem sentido para encontrar o resultado de problemas que não sabem interpretar.
Discussão
O problema da notação matemática é apenas um dos problemas que professores e alunos têm que enfrentar no aprendizado da matemática. Há muitas outras coisas que podemos pensar a partir das considerações que fizemos neste capítulo:
Em 1621, o matemático francês Claude Gaspard Bachet de Mériziac (1581 – 1638) editou a Aritmética, de Diofanto, em latim e grego. Pierre de Fermat (1601 – 1665), o matemático amador mais celebrado de todos os tempos, possuía um exemplar dessa edição. Conta-se que, em uma de suas leituras, ao lado de um problema algébrico, Fermat escreveu nas margens de sua cópia: “Se um número inteiro n for maior que 2, então a n + b n = c n não terá soluções para inteiros a, b e c diferentes de zero. Tenho uma prova verdadeiramente maravilhosa dessa proposição, mas essa margem é muito estreita para a conter.” Esse é o famoso Último Teorema de Fermat , demonstrado em 1995 pelo matemático inglês Andrew Wiles. Mas a questão aqui é outra: Fermat lia um livro escrito 1.400 anos antes. Será que o ensino de matemática seria mais bem-sucedido, e os alunos mais criativos, se pudéssemos ler as obras originais dos matemáticos?
Que outros problemas com a linguagem matemática você consegue identificar? Você chegou a ter problemas com ela?
Até mesmo em aulas de geometria, problemas são frequentemente traduzidos em álgebra e resolvidos mecanicamente, sem nenhum apelo a noções geométricas ou intuições espaciais. Seria a álgebra, pelo seu caráter mecânico e regular, a origem da morte do significado nas aulas de matemática?
Hipácia e o fim da tradição matemática grega

O filme Ágora , de 2009, dirigido por Alejandro Amenábar, apresenta-nos a premiada atriz Rachel Weisz como Hipácia de Alexandria (c. 351/370 – 415). Weisz conseguiu, com uma atuação brilhante, captar a genialidade e a vivacidade daquela que é considerada a primeira cientista da história ocidental e, ao mesmo tempo, a última diretora da magnífica Biblioteca de Alexandria.
Versada em astronomia e matemática, assim como em filosofia, poesia e artes, Hipácia era filha de Téon de Alexandria (335 – 395), outro renomado matemático e astrônomo da época. Hipácia em muito superou o pai, tendo escritos tratados sobre Diofanto, Ptolomeu e Euclides. Assumiu também a direção, com apenas 30 anos, da lendária Biblioteca de Alexandria, o grande centro da cultura e da ciência helenísticas.
Conta-se que Hipácia era exímia nas técnicas de resolução de problemas de matemática, habilidade que empregou no aperfeiçoamento do hidrômetro e na criação do astrolábio plano. Escreveu muito, mas nenhuma de suas obras sobreviveu. É provável, no entanto, que seus livros tenham sido assinados por cientistas homens, uma vez que a situação de subalternidade imposta às mulheres tem raízes profundas e remotas. Embora a educação universitária moderna seja composta majoritariamente por mulheres, ainda hoje poucas obtêm reconhecimento nas ciências exatas.
Um drama frequentemente relatado sobre a vida de Hipácia é sua morte dramática. Mulher não cristã com posição de destaque na sociedade alexandrina de seu tempo, Hipácia entrou em conflito com o fanatismo religioso e anticientífico de Cirilo (375/378 – 444), o patriarca da cidade, preocupado com o expurgo de doutrinas e ideias que afrontavam os dogmas da cristandade. Para neutralizar Hipácia, Cirilo espalhou boatos de que ela fazia sacrifícios humanos. Em uma tarde de março de 415, ela foi arrastada por uma turba de cristãos furiosos até uma igreja e lá dentro torturada cruelmente, tendo seu corpo lançado às chamas logo depois. Uma consequência dessa tragédia é que a Biblioteca de Alexandria seria fechada, tendo perdido sua última e mais brilhante diretora.
A morte de Hipácia marca tanto o fim do período helenístico nas ciências quanto o início da Idade Média, ainda que a filosofia grega continuasse a ser cultivada em escolas esparsas pela Europa e pelo norte da África. Mais de um milênio se passaria até que uma outra mulher voltasse a figurar na lista de grandes cientistas ocidentais.
Pouco mais de um século depois da morte de Hipácia, o pêndulo científico se voltaria para uma civilização de ideias mais arejadas que se formava bem ali perto, uma que viria a conquistar toda a região: a civilização árabe.
Discussão
A vida e morte de Hipácia suscitam uma série de questões interessantes, dentre as quais as seguintes:
Por que você imagina que existam tão poucas mulheres de destaque nas ciências exatas?
Em Alexandria e em sua Biblioteca, floresceram dezenas de gerações de cientistas por mais de sete séculos. Seria o subdesenvolvimento crônico do povo brasileiro apenas uma consequência da falta de bibliotecas na maioria de nossas cidades?
O que você pensa do multimilenar conflito entre ciência e religião? Sabemos que ciência e religião não estão necessariamente em conflito, mas que existem, de fato, afirmações em diversos livros sagrados que contradizem frontalmente os mais elementares conhecimentos científicos. O que você pensa que deve ser feito nessas horas?
Zero

Disputas históricas raramente são definitivas. Até que novos documentos e vestígios sejam descobertos e novas interpretações sejam propostas, a história oficial se mantém em uma espécie de limbo narrativo, aguardando ser reescrita por jovens historiadores em busca de um lugar ao sol. Com a história do zero não é diferente.
É discutível se os matemáticos do Egito e da Mesopotâmia conheciam o conceito de zero, mas certamente não possuíam um símbolo para representá-lo. No Egito, construtores marcavam o nível do solo, o nível zero, com um símbolo, mas esse símbolo não era usado em seu sistema de numeração. Os astrônomos da Mesopotâmia deixavam espaços no meio dos números para indicar o zero, o que, obviamente, gerava um enorme problema de leitura. Como saber, por exemplo, se o número 2 1 era 21, 201 ou 2001? Além disso, um simples número como 3 poderia indica 3, 30, 300 ou mais, pois nunca sabemos quantos espaços à direita o escriba teve a intenção de deixar.
Todo esse problema aparece quando usamos a notação posicional para registrar números, ou seja, quando um mesmo algarismo tem valor diferente dependendo da posição que ocupa. O número 55 é feito por dois algarismos iguais, mas o da esquerda vale dez vezes mais do que o da direita. A numeração romana que usamos ainda hoje não é estritamente posicional, e este é apenas um dos sistemas criados na história em que a posição não desempenha papel fundamental.
Apenas no século passado, historiadores europeus voltaram seus olhos para as contribuições científicas de povos distantes da bacia mediterrânea, como indianos, chineses e maias. O interessante é que foram exatamente esses os primeiros a reconhecer a utilidade de um símbolo para o zero em suas notações.
Por volta de 665, os maias já tinham um símbolo para o zero. Mas, por razões óbvias, isso não influenciou em nada a ciência do Velho Mundo. Coube aos indianos realizar o feito de reinventar e difundir um símbolo para o zero.
O zero já era comum na matemática indiana por volta do ano 650, uma época de ouro para as ciências naquela região. Três matemáticos se destacavam: Brahmagupta (c. 598 – c. 668), Bhaskara (c. 600 – c. 680), conhecido por sua célebre forma, e Mahavira (c. 800 – c. 870), já de uma geração posterior. Todos os três usavam o zero em operações matemáticas. Brahmagupta afirmava, por exemplo, que um número subtraído dele mesmo resultava em zero, e que qualquer número multiplicado por zero é zero. Isso nos parece demasiadamente óbvio hoje, mas foi um grande feito para a época.
Levado ao Ocidente pelos árabes, o símbolo para o zero dos matemáticos indianos era como o nosso, apenas menor e elevado na linha de escrita. Foi apenas em 1202, com o Liber Abaci (O livro do ábaco), de Leonardo de Pisa (c. 1170 – c. 1240/1250), que os algarismos indo-arábicos fizeram sua entrada definitiva na ciência ocidental, desbancando as terríveis dificuldades das operações com os números romanos ou com as pedrinhas usadas nos ábacos medievais da época.
Discussão
Livros inteiros foram escritos para tratar da invenção do zero. Vamos pensar um pouco mais sobre ele e sobre sistemas de numeração com as seguintes questões:
O zero é importante não só na aritmética, mas também na álgebra. Você consegue imaginar outras utilidades para ele além daquelas descritas aqui?
Existem diversos sistemas de numeração no mundo, tanto históricos quanto modernos, com diversas bases. O nosso, de base 10, possui 10 símbolos distintos. Outro, muito usado na moderna computação, usa a base hexadecimal, com todos os conhecidos 10 algarismos indo-arábicos mais as letras A, B, C, D, E e F. Pesquise por que foram criados e responda: seria conveniente introduzir esse sistema nas escolas básicas para melhor adaptar os alunos ao universo da moderna computação?
Tente somar os números romanos CCXXIX com DXLVIII, sem convertê-los para decimais, e diga se isso tornou seu dia mais feliz – ou não.
Alcuíno e suas Propositiones

Não é a primeira vez que escrevo sobre uma personalidade que ainda me enche de admiração e respeito. Alcuíno de York (735 – 804), o “Ministro da Educação e da Cultura”, por assim dizer, do imperador Carlos Magno (742 – 814), foi uma figura central na reorganização dos conhecimentos medievais, uma mescla de conhecimentos da Antiguidade com as contribuições cristãs, preparando terreno para as futuras universidades europeias, em uma época quando já existiam universidades muçulmanas no norte da África.
Alcuíno não foi uma figura de destaque na história da matemática. Olhá-lo dessa maneira é diminuir sua importância como o grande reformador que foi. Monge formado em York, na Grã-Bretanha, Alcuíno foi convidado pelo imperador dos francos, Carlos Magno, para reformar as escolas do império, dando origem a um período chamado de Renascimento Carolíngio . Alcuíno também teve uma influência decisiva em várias decisões políticas de Carlos Magno, a quem aconselhava com frequência.
Alcuíno era visto como um excelente professor. Sua grande contribuição foi retomar a estruturação dos conhecimentos da época segundo o modelo clássico, dividido em dois grandes ramos, o trívio , composto de gramática, lógica e retórica, e o quadrívio , que englobava aritmética, geometria, astronomia e música. Conjuntamente, esses conhecimentos eram conhecidos desde a antiguidade como as sete artes liberais , e continham a divisão que vemos até hoje entre ciências humanas e exatas.
Na história da matemática, Alcuíno é conhecido por ter sido o compilador e editor das famosas Propositiones ad Acuendos Juvenes (Proposições para aguçar o espírito da juventude), um conjunto de 53 problemas de matemática elementar que tratam de aritmética, álgebra, geometria, lógica e até algumas “pegadinhas” para divertir o leitor. Você pode ler na íntegra o texto das Propositiones no link https://fredlopes.com.br/matematica/historia-da-matematica/ em tradução direta do latim medieval. Como sempre, é melhor pôr a mão na massa do que simplesmente vê-la fermentar. Então eis aqui cinco problemas das Propositiones , para nossa mui grande alegria:
Proposição 1
Uma lesma foi convidada por uma sanguessuga para um jantar a uma légua de distância. Mas ela não pôde andar mais do que uma só polegada por dia. Diga, quem queira, quantos dias a lesma andou para esse jantar.
Proposição 18
Um homem devia levar para o outro lado do rio um lobo, uma cabra e um molho de couve, mas não pôde outro barco encontrar senão um que podia levar apenas dois deles. E lhe foi dito que chegassem ilesas do outro lado todas essas coisas. Diga, quem pode, como ele pôde transferi-los ilesos para o outro lado.
Proposição 41
Um pai de família construiu um chiqueiro quadrangular novo, no qual pôs uma porca, que pariu 7 porquinhas no meio do chiqueiro, que, acompanhada da mãe, que era a oitava, pariram cada uma 7 em cada ângulo. E ela novamente com todos os gerados pariu 7 no meio do chiqueiro. Diga, quem deseja, quantos porcos havia junto com a mãe.
Proposição 42
Há uma escada que tem 100 degraus. No primeiro degrau pousava uma pomba, no segundo duas, no terceiro 3, no quarto 4, no quinto 5. E assim em todos os degraus até o centésimo. Diga, quem pode, quantas pombas havia no total.
Proposição 43
Um homem tinha 300 porcos e ordenou que todos os porcos deveriam ser mortos em números ímpares em 3 dias. O mesmo também se fossem 30. Diga, então, quem pode, quantos porcos em número ímpar de 300 ou de 30 devem ser mortos em 3 dias.
Discussão
A matemática medieval não cessa de surpreender os pesquisadores, que sempre se veem diante de novos textos e interpretações. O que você pensa do seguinte:
A primeira proposição, como vemos, é totalmente irrealista, como muitas outras. No entanto, é uma história que diverte, principalmente quando nos surpreendemos com a resposta. Isso sempre nos leva a questionar se não seria melhor ensinar através de histórias interessantes e divertidas do que com exemplos concretos e “contextualizados”. O que você acha disso? (A propósito: uma légua tem 90.000 polegadas, e cada polegada mede 2,54 cm.)
Existe uma história sobre o matemático alemão Carl F. Gauss (1777 – 1855) que conta que ele resolveu, com a tenra idade de 10 anos, o problema de somar todos os números de 1 a 100 em apenas alguns segundos. O problema em questão é equivalente à proposição 42 acima, que Gauss o resolveu com o mesmíssimo método de Alcuíno. Será que Gauss conhecia as Propositiones ? Ou será que a “descoberta” de Gauss não era assim tão genial, sendo contada como mais uma daquelas muitas anedotas e lendas criadas para transformar matemáticos demasiadamente humanos em semideuses do pensamento?
Que solução você encontrou para a proposição 43? O que Alcuíno disse sobre isso?
Al-Khwarizmi e a álgebra

Apenas um matemático em toda a história foi capaz de emprestar seu nome a dois importantes conceitos e ter o título de seu principal livro com o nome de toda uma ciência: Abū Jafar Muḥammad ibn Mūsā al-Khwārizmī (c. 780 – c. 850). De seu nome, também escrito em português como Alcuarismi, temos as palavras algarismo e algoritmo , e de seu mais importante tratado matemático, o Al-Kitāb al-mukhtaṣar fī ḥisāb al-jabr wa-l-muqābala (c. 823), temos o nome álgebra. Mas quem foi esse matemático e do que tratava seu livro?
Al-Khwarizmi nasceu por volta de 780 na região de Khwarizm, no atual Uzbequistão. Seu nome é Abu Jafar Muḥammad ibn Musa, e Al-Khwarizmi, apenas o seu gentílico, o nome que indica o local de seu nascimento. Sabemos assim que Al-Khwarizmi era de ascendência persa nascido em uma região sob o domínio árabe.
Pouco mais do que fatos esparsos sabemos de sua vida. Do que temos certeza é que Al-Khwarizmi foi astrônomo e diretor da Bayt al-Hikmah, a Casa da Sabedoria , uma biblioteca e um centro de tradução fundada pelo lendário califa Harun al-Rashid (763/766 – 809) na brilhante Bagdá, capital do Iraque, uma cidade absolutamente central na história das ciências e na preservação da antiga ciência grega, cidade hoje barbarizada e saqueada pelos Estados Unidos e seus aliados nas guerras pelo petróleo.
Em Bagdá, Al-Khwarizmi escreveu sobre astronomia, geografia e cartografia, mas principalmente sobre matemática. Seu livro Al-Kitāb al-mukhtaṣar fī ḥisāb al-jabr wa-l-muqābala (Livro Compêndio sobre Cálculo por Restauração e Balanceamento) foi responsável por estabelecer a álgebra como uma disciplina independente a ser estudada com seus próprios princípios e regras. Ao reduzirmos seu título para Al-Kitāb al-jabr wa-l-muqābala (Livro da Restauração e do Balanceamento), conseguimos ver na palavra central ( al-jabr ) a origem da nossa palavra álgebra .
Mas o que significam restauração e balanceamento? Em termos modernos, simplesmente as operações usuais de agrupar e transpor os termos nos dois lados de uma equação. Com essas operações, hoje cansativamente conhecidas, Al-Khwarizmi desenvolveu métodos sistemáticos para encontrarmos as raízes de equações lineares e quadráticas . Apresentou também, de forma notável, o método do completamento de quadrados , que nos possibilita resolver equações quadráticas (modernamente chamadas de equações de segundo grau) sem a necessidade de utilizarmos a famigerada fórmula de Bhaskara.
Al-Khwarizmi conhecia bem os algarismos indo-arábicos, tendo até escrito um livro sobre eles. Mas, curiosamente, ele não os utilizou, assim como nenhum outro símbolo, em sua Álgebra , onde até os números eram escritos por extenso. Aparentemente, foi um retrocesso em relação à notação de Diofanto, mas é o conteúdo do livro que nos mostra que ocorreram avanços. O que nos faz pensar sobre a (des)importância dos símbolos no pensamento matemático.
Discussão
A civilização árabe contribuiu (e contribui) de forma decisiva para as ciências. Infelizmente, temos pouco acesso às suas contribuições, dada a dificuldade da língua. Mas podemos pensar muitas outras coisas:
Os árabes criaram a Casa da Sabedoria para preservar e traduzir obras científicas e filosóficas de todos os cantos do mundo. Muitas das principais obras da ciência grega existem hoje somente em língua árabe. Mas por que criar um lugar assim?
Observe esse problema que aparece na Álgebra de Al-Khwarizmi: “Você divide dez em duas partes: multiplique uma por si mesma. Essa será igual à outra multiplicada oitenta e uma vezes. ” Você é capaz de dizer quais partes são essas?
Al-Khwarizmi não precisou de símbolos especiais para fazer matemática. Será que a matemática precisa mesmo de símbolos diferentes das palavras da linguagem natural?
Omar Kayyam, a poesia e a matemática

Aos céus enviei minha alma
Em busca do segredo eterno…
Na volta, me diz, já bem calma:
‘Eu mesma sou Céu e Inferno’
Do Rubaiyat
Omar Khayyam nasceu em maio de 1048 na rica e próspera Nixapur, no nordeste do Irã, tendo ali vivido e morrido, em dezembro de 1131, após uma vida de grandes realizações.
Khayyam é uma das personalidades iranianas mais conhecidas em todo o mundo. Não pelos seus feitos científicos, mas por sua obra poética mais conhecida: o Rubaiyat , uma coleção de quadras que versam sobre a alegria e o sentido de viver. A que abre este texto é uma transcriação que fiz a partir da tradução de E. Fitzgerald, a mais utilizada em língua inglesa. Existem várias traduções em português, partindo de versões inglesas ou francesas, mas nenhuma direta do persa. Alguém aí se habilita?
Embora famoso por sua obra poética, Khayyam não fica atrás em seus feitos científicos. A página mostrada no início deste capítulo faz parte de um tratado sobre a resolução de equações cúbicas através da interseção de cônicas . Embora o material fosse já conhecido, Khayyam generalizou os métodos e os aplicou com bastante sucesso, fazendo avançar as técnicas de solução de equações polinomiais.
Khayyam conhecia uma fórmula para calcular os coeficientes da expansão de (a+b) n . Por exemplo, os coeficientes de (a+b) 5 = a 5 +5a 4 b+10a 3 b 2 +10a 2 b 3 +5ab 4 + b 5 são 1, 5, 10, 10, 5 e 1, e Khayyam sabia como calcular cada um deles sem realizar a expansão de (a+b) 5 . Para os mais astutos, esses coeficientes fazem a sexta linha do famoso triângulo de Pascal , conhecido por árabes, indianos e chineses séculos antes do filósofo e matemático Blaise Pascal (1623 – 1662) ter nascido. Se você acha que há muito nome europeu indevidamente na matemática, saiba que não está só!
Outra área em que Khayyam se destacou foi na geometria, principalmente pelo seu livro Sharh ma ashkala min musadarat kitab Uqlidis (Comentários sobre as Dificuldades nos Postulados no Livro de Euclides). Nessa obra, Khayyam discute o famoso quinto postulado de Euclides e tropeça nas geometrias não-euclidianas, um ramo da matemática que floresceria somente sete séculos depois.
Discussão
Quão grandes foram as contribuições da atual Irã para a matemática? E as contribuições da Ásia em geral?
Os contatos comerciais por toda a Ásia sempre foram fortes e intensos, levando ao desenvolvimento cultural e científico de muitas regiões. Você acha que povos asiáticos possuíam uma ciência mais avançada do que a ciência ocidental à época de Khayyam?
Hoje chamamos astrônomos, geômetras e algebristas da antiguidade de matemáticos, embora eles mesmos não usassem esse termo. Você acha que é correto ou não chamá-los assim?
Por que você acha que o tema dos postulados de Euclides foi tão discutido durante a história da matemática?
Fibonacci e seu Liber Abaci

Leonardo de Pisa (c. 1170 – c. 1240/1250) é o mais interessante matemático do século XIII. Nascido em Pisa, na Itália, mudou-se ainda jovem com o pai, Guglielmo dei Bonacci, para a cidade de Bugia, na Argélia, onde passou parte de sua vida. Matemático e escritor, é autor do influente Liber Abaci (Livro do Ábaco), obra que temos a oportunidade de conhecer a seguir.
Ter morado na Argélia, no norte da África, não é um detalhe na vida de Fibonacci. Pelo contrário, é sua parte mais importante: foi no milenar porto de Bugia, onde eram embarcadas as mercadorias vindas do Oriente em direção à Europa, que Leonardo, posteriormente apelidado Fibonacci (de filho de Bonacci ), deu início a seus estudos da matemática ágil usada pelos árabes em suas transações comerciais.
Compelido por sua prática de comerciante, Fibonacci foi estudar em Constantinopla, onde aprendeu principalmente nos livros de Al-Khwarizmi e de muitos outros matemáticos árabes. Tomou contato com os algarismos indo-arábicos e com as técnicas de cálculo facilitadas por eles. Lembremo-nos de que na Europa, naquela época, as operações aritméticas que hoje realizamos com facilidade eram laboriosamente feitas com ábacos e algarismos romanos. Toda essa tradição de cálculo seria rapidamente esquecida com a introdução das novas técnicas que Fibonacci levaria em seu mais conhecido livro.
No Liber Abaci (pronunciamos líber ábaki ), Fibonacci introduz o modo dos hindus , a maneira como os indianos realizavam operações. No início de seu livro, escreve:
Estas são as nove figuras dos Indianos:
9 8 7 6 5 4 3 2 1
Com estas nove figuras, e com o sinal 0, que em árabe é chamado de zéfiro, qualquer número pode ser escrito.
Mas os números ainda não tinham esse formato. Basta uma olhadela na página que ostenta o famoso problema dos coelhos , no início deste texto, para constatarmos que os formatos de nossos algarismos ainda sofreriam algumas mutações. E, em verdade, não foi a primeira vez que apareceram na Europa: o matemático Gerbert d’Aurillac (c. 950 – 1003), que se tornaria o papa Silvestre II, já os conhecia e com eles operava, cerca de duzentos anos antes.
Levaria ainda algum tempo para que o Liber Abaci exercesse alguma influência nas práticas de cálculo de seu tempo. Fibonacci escreveria outros livros, como o Practica Geometriae (Prática de Geometria), o Flos (Flor) e o Liber Quadratorum (Livro dos Quadrados), mas apenas o Liber Abaci seria destinado tanto a acadêmicos quanto a comerciantes.
É nesse livro que surge o famoso problema dos coelhos , que dá origem à sequência de Fibonacci , objeto de admiração e estudo por amadores e matemáticos profissionais, dada sua aparente onipresença em muitas áreas da matemática pura e aplicada, assim como na física, na química, na biologia, nas engenharias e até nas artes. O problema é o seguinte:
Quantos pares de coelhos são gerados a partir de um par em um ano?
Alguém põe um par de coelhos em um certo lugar totalmente cercado por um muro para saber quantos pares de coelhos são gerados a partir desse par inicial em um ano. A natureza desses coelhos é tal que a cada mês um par de coelhos produz outro par, e coelhos começam a gerar coelhos a partir do segundo mês após seu nascimento.
Sua solução dá origem à sequência
1 2 3 5 8 13 21 34 55 89 144 233 377…
à qual foi acrescentada os números 0 e 1, passando a ser escrita como
0 1 1 2 3 5 8 13 21 34 55 89 144 233 377…
Essa sequência é formada recursivamente : a soma de dois números sucessivos forma o terceiro. Por exemplo: 0 + 1 = 1 , 1 + 1 = 2 , 1 + 2 = 3 , 2 + 3 = 5 , 3 + 5 = 8 e assim sucessivamente. Observe que a sequência apresenta um padrão do tipo par-ímpar-ímpar : 0, 1, 1, depois 2, 3, 5 e assim por diante. Observe também que, se pegar o número seguinte e dividir pelo número anterior, você formará uma sequência que se aproximará do número 1,618…:
8/5 = 1,6…
13/8 = 1,625…
21/13 = 1,615…
34/21 = 1,619…
55/34 = 1,617…
89/55 = 1,618...
e assim por diante, convergindo para aquele que é visto como um dos mais notáveis números da matemática, a constante ϕ=1,61803398875… (pronunciamos fi ).
Essa constante surge no antigo problema de se dividir um segmento em média e extrema razão, que significa encontrar um ponto em um segmento que o divida em duas partes, uma maior e uma menor, de tal maneira que a razão (divisão) do segmento todo pelo segmento maior é a mesma razão (divisão) do segmento maior pelo segmento menor. Essa é a chamada razão áurea .
Embora pareça abstrata, a razão áurea é usada por alguns artistas para dar um certo balanço em suas obras, sejam elas literatura, música ou artes visuais. Há quem diga que ela aparece nas proporções de tudo o que é belo e equilibrado, tanto na natureza quanto nas obras humanas, afirmação que beira mais a superstição do que a evidência científica. No entanto, é verdade que ϕ aparece aqui e ali em belíssimos teoremas da geometria e da teoria dos números. Mas a única evidência que temos, depois de pesquisarmos com calma o assunto, é que basta um empurrãozinho em mentes menos críticas para provocar uma avalanche de crendices populares.
O Liber Abaci também lida com medidas, moedas, cálculo de lucro e de juros, números perfeitos, números primos e compostos, números irracionais, extração de raízes e algumas demonstrações de geometria. É um livro de interesse tanto prático quanto teórico, o que garantiu sua sobrevivência e utilidade pelos séculos seguintes. Como muitos outros livros interessantes da história, não conhece sequer cheiro de tradução para o português…
Discussão
Bem no início do Renascimento europeu, encontramos uma figura como Fibonacci, que nos mostra claramente o quão intensa era a dinâmica de trocas culturais ao redor da bacia mediterrânea. Há muito o que aprender com essa época, mas, por ora, fiquemos com essas questões:
Como você acha que Fibonacci resolveu o problema dos coelhos?
O ábaco é um instrumento que assume muitas formas em diferentes países. É bastante utilizado na educação básica com muito bons resultados. Aprenda a operar um deles, o soroban (ábaco japonês), e teste seus conhecimentos fazendo 437 + 585.
A sequência de Fibonacci é tão admirável que um exército de amadores e profissionais passaram a vê-la em muitos lugares. Um desses é na natureza: na inflorescência do girassol, nas proporções dos animais e até nos braços da galáxia. Toda a natureza se estruturaria segundo “padrões de Fibonacci”: a matemática está mesmo em tudo ou somos nós que queremos vê-la assim, onipresente?
Cardano, a álgebra e a probabilidade

Se algo existe que nos faça pensar em não utilizar fontes primárias no ensino de matemática, esse algo é o livro Ars Magna , do médico, matemático, astrólogo e jogador inveterado italiano Girolamo Cardano (1501 – 1576), um livro moroso e entediante em franco contraste com a vida de seu autor.
Cardano nasceu em 1501 em Pavia, na Itália, e formou-se em medicina em 1525 na Universidade de Pádua. Exerceu a profissão de médico em cidades pequenas até se mudar para Milão, onde obteve licença para ensinar matemática, paixão intelectual que o perseguiu até seus últimos dias. Embora tenha escrito cerca de 200 obras sobre medicina, biologia, física, química, astronomia, mecânica, filosofia e até astrologia, foi na matemática que se mostrou mais proficiente e mais fecundo.
Sua obra mais conhecida é a Artis magnae, sive de regulis algebraicis (Da grande arte, ou sobre as regras da álgebra), a que nos referimos simplesmente como Ars Magna . Nela encontramos a primeira publicação de soluções puramente algébricas de equações cúbicas e quárticas , equações polinomiais de graus 3 e 4, respectivamente. Cardano, no entanto, não foi seu descobridor: ele atribui a Scipione del Ferro (1465 – 1526) a solução da cúbica e a seu aluno Ludovico Ferrari (1522 – 1565) a da quártica.
É preciso parar e observar que esse foi um momento muito importante na história da matemática. A solução de equações polinomiais de qualquer grau é uma busca milenar que começou na antiguidade, tendo ocupado gerações e gerações de matemáticos amadores e profissionais. Com Cardano, as equações de graus 1, 2, 3 e 4 foram definitivamente solucionadas. Foi o passo seguinte, a busca da solução da equação de quinto grau, a quíntica , que ocasionou a criação da moderna álgebra abstrata . Niels Abel (1802 – 1829) e Evariste Galois (1811 – 1832) foram os responsáveis por demonstrar, independentemente, que a quíntica só possui soluções para casos particulares, ficando o caso geral ax 5 + bx 4 + cx 3 + dx 2 + ex + f = 0 sem uma fórmula que o resolva.
Outro fato interessante da história da matemática do período é saber que os números negativos, hoje tão comuns, ainda não eram bem-aceitos àquela época. Historicamente ligado às ideias de quantidade e de magnitude, o conceito de número não admitia algo “menor do que o nada”, engano comum entre os estudantes de matemática ainda hoje. Essa proibição cognitiva obrigou Cardano, assim como todos os matemáticos da época, a tratar equações do tipo x 3 + ax = b de maneira diferente de equações do tipo x 3 = ax + b, o que hoje resolvemos com o mesmo método. No entanto, ele, de fato, operou formalmente com números negativos e, de maneira desconcertante, também com números complexos, aqueles que envolviam raízes de números negativos.
Na
Ars Magna
, Cardano apresenta o seguinte problema: encontre dois números tais que sua soma seja 10 e seu produto seja 40. As respostas são
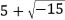 e
e
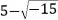 , que Cardano chamou de “sofísticas”, pois não viu nelas nenhum significado físico. Mesmo assim, Cardano foi adiante, realizou as contas, corajosamente, e viu que as soluções satisfaziam as condições do problema. Apesar do sucesso, declarou que essas respostas seriam tão sutis quanto inúteis. Esta foi a primeira aparição de números complexos em uma obra impressa.
, que Cardano chamou de “sofísticas”, pois não viu nelas nenhum significado físico. Mesmo assim, Cardano foi adiante, realizou as contas, corajosamente, e viu que as soluções satisfaziam as condições do problema. Apesar do sucesso, declarou que essas respostas seriam tão sutis quanto inúteis. Esta foi a primeira aparição de números complexos em uma obra impressa.
Cardano era um jogador contumaz e um enxadrista talentoso, o que lhe rendeu um bom dinheiro durante sua vida, o suficiente para saldar as múltiplas dívidas que sistematicamente contraía. Como não poderia deixar de ser, escreveu também sobre jogos no Liber de ludo aleae (Livro dos jogos de azar), que contém o primeiro tratamento sistemático da probabilidade , outro grande debate da época. Mas o que torna esse livro impertinentemente delicioso são as muitas técnicas para trapacear em diversos jogos, um brinde de Cardano à vida de apostador que ele adorava viver.
Discussão
O que um simples jogo de cartas pode contribuir para a matemática e a análise de riscos? Nada menos do que a criação da teoria das probabilidades, um capítulo à parte na história da matemática. Sem querer adentrar esse terreno, fique com estas questões bem mais simples:
Além de cientista, Cardano era também astrólogo, tendo feito inúmeros mapas astrais para os poderosos da época. Sabemos hoje que a astrologia é uma pseudociência sem a mínima chance de voltar a ter o respeito que teve antigamente. Mas ainda é extremamente popular. O que você pensa disso?
Você consegue imaginar um argumento que justifique tanta energia empregada, durante tanto tempo, para resolver equações polinomiais?
Se um número não é a medida de uma quantidade, então o que ele é?
Bombelli e os números complexos

Há cerca de 500 anos, quando matemáticos ainda se debatiam com números negativos, uma nova classe de números ainda mais estranha surgia: os números complexos . Apesar de realizarem seu début na obra de Cardano, coube a Rafael Bombelli (1526 – 1572) iniciar o primeiro estudo sistemático desses objetos que viriam revolucionar o conceito de número.
Bombelli foi um engenheiro talentoso que viveu em um ambiente intelectual onde as mais avançadas técnicas algébricas estavam facilmente disponíveis. Fazendo bom uso de sua mentalidade prática, escreveu um livro que pode ser lido ainda hoje por leigos e profissionais. Editado no mesmo ano da morte de seu autor, em 1572, essa obra possui o título originalíssimo de… Algebra .
Possuidor da rara virtude de ser claro e acessível, esse livro fez com que Bombelli se tornasse o primeiro europeu a escrever as regras de operação com números inteiros :
Mais vezes mais faz mais.
Menos vezes menos faz mais.
Mais vezes menos faz menos.
Menos vezes mais faz menos.
Mais 8 vezes mais 8 faz mais 64.
Menos 5 vezes menos 6 faz mais 30.
Menos 4 vezes mais 5 faz menos 20.
Além disso, 5 vezes menos 4 produz menos 20.
Da Algebra, de Bombelli
Mais do que pelo seu trabalho com inteiros, Bombelli se destaca na história da matemática por ter sido o primeiro a operar com números complexos , aqueles que envolvem raízes de números negativos.
Bombelli teve a presciência de perceber como os complexos eram essenciais na resolução de cúbicas e quárticas e possivelmente em outros problemas. Ele introduziu a simbologia
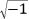 , que, mais tarde, viria a ser simplificada para
i
por L. Euler (1707 – 1783), para dar um perfil manuseável a esses números.
, que, mais tarde, viria a ser simplificada para
i
por L. Euler (1707 – 1783), para dar um perfil manuseável a esses números.
Bombelli sabia que os complexos eram potencialmente problemáticos. Entendia que não eram positivos nem negativos, e também que considerá-los como simples raízes era uma fonte de confusão – o que, de fato, aconteceu com os matemáticos dos séculos seguintes. Ao chamar
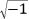 de “mais de menos” e
de “mais de menos” e
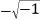 de “menos de mais”, Bombelli forneceu as regras formais de operação que usamos ainda hoje, revelando a índole mecânica da álgebra, que não necessita de significados concretos para funcionar perfeitamente. Além disso, os complexos nos mostraram que pensar números como representações de quantidades ou magnitudes é tão falso quanto imaginar que lógica e leis do pensamento são sinônimas.
de “menos de mais”, Bombelli forneceu as regras formais de operação que usamos ainda hoje, revelando a índole mecânica da álgebra, que não necessita de significados concretos para funcionar perfeitamente. Além disso, os complexos nos mostraram que pensar números como representações de quantidades ou magnitudes é tão falso quanto imaginar que lógica e leis do pensamento são sinônimas.
Os números complexos são absolutamente essenciais na matemática pura e aplicada. Aparecem na solução de diversos tipos de equações diferenciais , presentes na maioria dos modelos que os cientistas criam sobre o mundo. Sem elas, você não estaria lendo este texto na tela de seu computador ou celular. Ao observar a imensa gama de suas aplicações, percebemos que são os bizarros complexos, para os quais temos imensas dificuldades em atribuir um sentido concreto, os mais práticos dos números que conhecemos.
Discussão
Matemática e arte? Um bom começo é aprender a operar com números complexos!
O que é um número?
Bombelli conseguiu escrever um livro que era, ao mesmo tempo, profundo e simples de se ler. Você consegue citar algum outro livro de matemática com essas qualidades?
Fractais, como aquele no início deste texto, são criados com a manipulação computacional de números complexos, e servem como uma das portas de entrada para a reflexão sobre arte e matemática. Por que será que tanta gente vê relações entre esses dois domínios aparentemente tão distantes?
Logaritmos

Uma experiência comum entre professores de matemática é ouvir de alunos a provocativa pergunta “para que serve?”. Uma experiência ainda mais comum entre os alunos que não fazem tais perguntas é suspeitar que quase toda a matemática que aprenderam não serve para absolutamente nada. Ambas as experiências são falsamente reforçadas quando o tema em questão são os logaritmos .
Foi o matemático escocês John Napier (1550 – 1617) que introduziu os logaritmos como expediente de cálculo para simplificar as tediosas operações com números de muitos dígitos, necessárias aos astrônomos e navegadores da época. Com os logaritmos, operações de multiplicação, divisão e exponenciação se transformam em simples adições, subtrações e multiplicações. Mas como?
Suponha que você necessite realizar a multiplicação 32 x 128 e tem, ao seu lado, uma tabela de potências de 2. Olhando a tabela, você percebe que 32 = 2 5 e 128 = 2 7 . Daí percebe que para multiplicar esses números basta somar os expoentes 5 e 7 e achar 12. Com esse valor, você olha de novo na tabela e vê que 2 12 = 4096, encontrando a resposta da multiplicação. Você evitou uma multiplicação com uma adição e três olhadelas em uma tabela.
Pareceu mais complicado do que realizar a multiplicação? Mas não é. Imagine multiplicar números como 3,476098 e 1,775369 dezenas de vezes durante o dia. Mais fácil seria transformar essas multiplicações todas em adições, olhando em uma tabela os expoentes de 3,476098 e 1,775369, somar esses expoentes e novamente olhar na tabela o número que corresponde ao expoente encontrado. Quando usados dessa forma, esses expoentes são chamados de logaritmos .
Napier viria a aperfeiçoar sua invenção com o auxílio do matemático inglês Henry Briggs (1561 – 1630) e, a partir de então, os logaritmos se tornariam o mais importante avanço nas técnicas de cálculo até a invenção do computador digital, cerca de 400 anos depois.
Napier dedicou muito do seu tempo para desenvolver instrumentos de cálculo. Além dos logaritmos, desenvolveu uma espécie de ábaco chamado carinhosamente de ossos de Napier . A figura no início deste post mostra como era um instrumento desse: tabelas de multiplicação eram incorporadas em hastes que, quando giradas, transformavam multiplicações em adições e divisões em subtrações, seguindo a mesma lógica dos logaritmos. Em versões mais avançadas, extraíam até raízes quadradas. Os ossos de Napier foram inspirados em ideias de matemáticos árabes e também nas de Fibonacci, mostrando, mais uma vez, a influência de ambos na cultura europeia.
Pouco antes das calculadoras eletrônicas, era comum encontrar engenheiros utilizando réguas de cálculo em seus projetos. Esses instrumentos fascinantes incorporavam os logaritmos em sua construção e possibilitavam rapidez e precisão de resultados, dispensando tabelas e cálculos manuais. Ainda hoje são interessantes como instrumentos didáticos, e é comum encontrá-las em laboratórios de matemática nas universidades.
Alguns professores se desviam da pergunta impertinente “para que serve” dizendo coisas como “no futuro você verá” ou “para desenvolver o raciocínio”. Além de frustrarem as ambições científicas dos alunos, respostas como essas concorrem para demonstrar a ignorância do professor e as deficiências de sua formação. Melhor seria dizerem – e procurarem mostrar – como os logaritmos são usados na escala Richter , que mede a intensidade dos terremotos; no cálculo do potencial hidrogeniônico , o famoso pH, que calcula acidez ou a basicidade das substâncias; no cálculo da complexidade computacional , que classifica algoritmos segundo sua dificuldade inerente; na música , com o cálculo dos intervalos musicais; no cálculo da entropia de um sistema, medindo seu nível de desordem; e no cálculo da dimensão dos fractais. Mas será que os professores não acharão que isso “complica demais as coisas”?
Discussão
Logaritmos surgem em todos os lugares na matemática. Mas por quê?
Os logaritmos surgiram devido a necessidades práticas dos cientistas. Você acha que toda matemática é criada a partir de alguma urgência pragmática?
Se os esforços dos matemáticos se concentraram, durante muito tempo, em construir máquinas que fizessem as contas mais tediosas para eles, por que você deveria aprender a realizá-las com lápis e papel?
Você consegue dizer alguma outra aplicação dos logaritmos além daquelas discutidas no texto?
Descartes e a geometria analítica
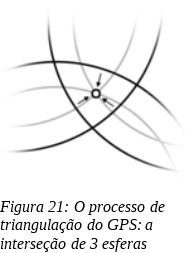
O GPS ( Global Position System – Sistema de Posicionamento Global), massivamente utilizado em aplicativos de transporte, foi uma invenção que teve início em 1957, quando a antiga União Soviética lançou o primeiro satélite da história – o Sputnik . A ideia de localizar objetos em terra a partir do espaço foi uma das motivações do projeto, mas foram os Estados Unidos que primeiro desenvolveram o sistema de localização, disponível a partir de 2000 para toda a população. O GPS faz uso, e de maneira até bem simples, de um sistema de coordenadas espaciais , provido pelo que hoje chamamos de geometria analítica .
A geometria analítica tem uma história antiga e, como todas as criações matemáticas, ela não surge completa e definitiva. Seu longo amadurecimento ocorreu nas mãos de matemáticos que precisavam localizar pontos e curvas no plano e no espaço a partir de uma referência. Esse referenciamento pode ser feito de várias maneiras, cada uma dando origem a um sistema de coordenadas . Os sistemas mais empregados hoje são o de coordenadas polares , largamente utilizado por Isaac Newton (1643 – 1727), e o de coordenadas cartesianas , assim nomeado em homenagem ao matemático francês René Descartes (1596 – 1650).
Talvez a mente mais lúcida de seu tempo, Descartes exerceu uma incomum influência na história das ideias. Principalmente preocupado em encontrar um fundamento sólido para todo o conhecimento, Descartes fazia parte da longa tradição de filósofos que buscavam as ideias mais básicas, certas e universais das quais tudo o mais se derivaria. Se você entendeu o que Euclides fez com sua estruturação lógico-dedutiva do conhecimento matemático, vai compreender o que Descartes procurou fazer, não só com a matemática, mas com todo o conhecimento humano.
Filósofo de coração, Descartes foi um matemático de grande talento. Ao editar La Géométrie (A Geometria) como um apêndice do seu mais importante livro, o Discurso do Método (1637), Descartes almejou libertar a geometria do uso de diagramas através de procedimentos algébricos e prover sentido geométrico às operações algébricas, fundindo ambas em um único corpo de conhecimentos.
Curiosamente, Descartes não usou o sistema de coordenadas cartesianas (!) ou nenhum outro sistema em sua Géométrie . No entanto, fixou o uso das letras x, y e z para variáveis e a, b e c para constantes; introduziu a moderna notação exponencial, como x 3 , x 4 , etc. (mas ainda escrevia xx para o que hoje escrevemos x 2 ); descreveu curvas em termos de suas equações e interpretou equações em termos de curvas, além de ter quebrado com o antigo princípio da homogeneidade, que escravizou a imaginação matemática a considerar x como um segmento e xx como uma área.
A “tradução” bidirecional entre geometria e álgebra operada por Descartes inspirou os matemáticos posteriores a procurar traduções entre outros campos e a criar métodos e soluções seguras para problemas que seguiam intratáveis até então. A álgebra, que opera de maneira mecânica com um conjunto pequeno e sólido de princípios e regras, garante a toda a matemática que nela se fundamenta segurança e solidez. E assim teve início, com a obra de Descartes, a mecanização moderna da matemática – em nosso benefício?
Discussão
Antes de matemático, Descartes era filósofo. Seria a matemática algum tipo de “filosofia exata”?
Você acredita que é possível encontrar os princípios primeiros do conhecimento humano, como Descartes pretendia? Quais princípios seriam esses?
O que você pensa do uso da álgebra em problemas de geometria? Acredita que seja uma coisa natural ou é algo que nos é imposto em função de alguma necessidade?
Será que toda a matemática pode ser mecanizável de maneira a ser melhor operada por computadores? É bom que assim o seja?
Newton e os infinitésimos

Isaac Newton (1642 – 1727), um cientista tímido e reservado, foi para o século XVIII o que Albert Einstein (1879 – 1955) foi para o século XX: um gênio que mudou o paradigma da ciência de seu tempo. Talvez ainda mais do que Einstein, Newton foi não só um criador de uma nova maneira de pensar a ciência natural, mas também um matemático original e profundo que forjou os instrumentos intelectuais do mundo moderno.
Há tanto o que falar de Newton, o último dos magos e o primeiro dos modernos, que toda escolha é uma severa ofensa a sua obra multifacetada. Todavia, limitaremos este texto a um aspecto de seu trabalho sobre uma das mais importantes ferramentas matemáticas da humanidade: o cálculo.
Foi no livro The Method of Fluxions (O método das fluxões), escrito em 1671 mas publicado postumamente em 1736, que Newton apresentou seu método das fluxões , o nome do que hoje conhecemos como derivadas. Derivadas estão no coração do chamado cálculo diferencial e integral e na raiz da revolução científica operada por Newton e seus contemporâneos. Mas por que são assim tão importantes?
Derivadas aparecem em todos os lugares. Quando medimos a velocidade em quilômetros por hora (km/h), a corrente elétrica em coulombs por segundo (C/s), a vazão em litros por segundo (l/s), estamos falando de derivadas. De maneira simplificada, Newton descobriu como, dada a equação da trajetória de um planeta, encontrar a equação de sua velocidade, e vice-versa. Newton derivou uma equação de outra, e essa foi a origem do nome derivada – nome que ele não utilizou.
Geometricamente, o problema envolve encontrar retas tangentes a curvas. O processo é simples uma vez entendido, mas criá-lo não foi nada fácil. Matemáticos, desde a antiguidade, desenvolveram métodos próprios para resolver problemas particulares, mas nenhum método geral que se aplicasse a todas as equações então conhecidas. Newton desenvolveu seu próprio método fazendo uso de um conceito controverso na história da matemática: os infinitésimos .
Tome um número positivo bem pequeno, mas que não seja zero. Suponha que esse número seja 0,01. É possível pensar um número menor? Sim, e até um dez vezes menor: 0,001. É possível pensar em um menor ainda? Sim: 0,0001, novamente dez vezes menor do que o anterior, e assim sucessivamente. Um infinitésimo é menor que todos esses números imagináveis e, ainda assim, não é zero. Como isso é possível?
No conjunto dos números reais, isso não é possível. Mesmo assim, Newton fez uso dos infinitésimos bem ciente de suas contradições. Empregou-os com coragem para resolver uma série de problemas persistentes, em linha com outros matemáticos de séculos anteriores que operaram com essas aparentes aberrações lógicas sem muitos pudores. Mas, por temer críticas e controvérsias, Newton postergou indefinidamente a publicação de seus resultados.
Vamos a um exemplo bem simples. Considere a equação mais simples de uma parábola, f(x)=x 2 , e considere que precisamos encontrar uma reta tangente em um ponto A(x, y) qualquer, como mostra a figura a seguir:
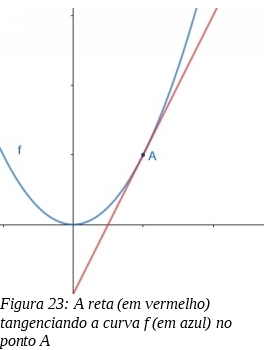
Em um determinado momento do processo de encontrar a derivada, Newton introduziria o infinitésimo “ o ” e faria o quociente
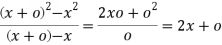
Depois, sem mais delongas, desprezaria o número “ o ” e encontraria a equação derivada 2x . O problema? Introduzir no processo algo diferente de zero e depois desprezá-lo como se fosse zero.
Newton sabia bem disso, como sabiam todos os matemáticos que utilizaram infinitésimos. Tudo funcionava maravilhosamente, mas ninguém conseguiu ignorar um elefante que surgiu na sala: o método parecia corroer as bases lógicas do edifício da matemática. Nunca na história das ciências um elefante tão diminuto causou tantos problemas.
Apesar dos contratempos, o método das fluxões continha os germes da ideia moderna de limites , usada para formalizar o conceito de derivadas e expulsar as contradições que os infinitésimos criavam. Mas, para isso, um complicado formalismo teve que ser introduzido no cálculo, gerando uma sopa de letrinhas intragável que os pobres coitados dos estudantes de exatas devem digerir nos modernos – e antipedagógicos – cursos universitários de cálculo.
Discussão
Há muito o que falar de Newton, mas fique, por ora, com essas questões:
Newton escreveu uma quantidade impressionante de artigos sobre alquimia e teologia, muito mais do que sobre física e matemática. No entanto, apenas estes últimos tiveram influência duradoura, enquanto os livros de teologia e alquimia foram esquecidos pela história. Por que você acha que isso aconteceu?
Os infinitésimos foram usados com sucesso durante séculos, antes e depois de Newton. Foram descartados pelos matemáticos do século XIX, preocupados com o rigor, e redescobertos na segunda metade do século XX. As contradições que geravam foram domadas e seu emprego foi reabilitado. Ainda assim, pouquíssimos os utilizam atualmente. Você acredita que ideias científicas têm seu tempo, e que, uma vez superadas, não é mais possível reutilizá-las?
Quais são os motivos para que as disciplinas de cálculo diferencial e integral sejam as maiores reprovadoras nas universidades?
O gênio de Leibniz

Contemporâneo de Newton, com quem se correspondeu, Gottfried Wilhelm Leibniz (1646 – 1716) foi uma dessas personalidades incontornáveis da história das ciências e da filosofia. Polímata de grande amplitude e profundidade, Leibniz foi outra figura central no desenvolvimento da matemática dos séculos XVII e XVIII. Mas não só dela: a lógica, a física, a biologia, a medicina, a psicologia, a linguística e a moderna computação lhe devem grandes tributos.
Como Newton, mas de maneira independente, Leibniz também desenvolveu sua versão do cálculo, tendo criado a notação mais utilizada atualmente. Seu cálculo era igualmente baseado em infinitésimos , geradores de desconcertantes contradições, mas Leibniz encarou o problema e buscou uma fundamentação clara e objetiva, dando os primeiros passos concretos para sua inclusão legítima no panteão matemático. No entanto, foi apenas na segunda metade do século XX, com a criação da análise não-standard por Abraham Robinson (1918 – 1974), que os infinitésimos foram finalmente reabilitados e puderam ser utilizados com tranquilidade pelos matemáticos — ainda que bem poucos o façam.
Leibniz era um lógico atento e profundo. Nesse terreno, fez uma contribuição fundamental: o princípio da identidade dos indiscerníveis , que afirma que duas coisas que têm o mesmo conjunto de propriedades são, na verdade, a mesma coisa. Junto com o princípio da não-contradição e o princípio da razão suficiente , esse é considerado um dos três grandes princípios da metafísica. Metodologicamente, ao transformar uma entidade na lista de propriedades que a definem, Leibniz nos deu uma lupa para a crítica social, uma vez que todas nossas ideias de universalidade passam por escolhas de propriedades comuns a classes de indivíduos, e essas escolhas não são naturais, mas ideologicamente motivadas.
Leibniz era também um gênio mecânico. Projetou e construiu a primeira calculadora capaz de realizar todas as quatro operações aritméticas, a Staffelwalze (contadora de passos):

Leibniz acreditava, como muitos cientistas ainda hoje, que cálculos laboriosos ocupam um tempo precioso de um pesquisador e que qualquer pessoa pode fazer a mesma coisa com o auxílio de uma máquina. A Staffelwalze , porém, tinha um projeto tão delicado e sutil de engrenagens, tão além das habilidades dos artesãos da época, que apenas duas cópias foram feitas. A Leibniz, que pretendia comercializá-la, coube apenas se conformar.
Fascinado com dispositivos mecânicos e com a automação de ações repetitivas, Leibniz pretendeu levar essas ideias para outros domínios de atividade humana. Imaginava, por exemplo, que contendas e disputas judiciais poderiam ser resolvidas se as partes conseguissem codificar suas demandas em uma espécie de linguagem a ser manipulada algebricamente, como em uma máquina, produzindo a solução do impasse.
A ideia de criar uma linguagem universal que codificasse os entes do mundo e suas relações ocupou Leibniz durante sua juventude e muito de sua vida adulta. Seus esforços nessa direção passaram tanto pela filosofia quanto pela matemática, e inspiraram a criação de línguas artificiais, como o esperanto, além de ter dado partida na moderna teoria da computação, que tem seu texto fundador no artigo Explication de l’arithmétique binaire, qui se sert des seuls caractères 0 et 1, avec des remarques sur son utilité, et sur ce qu’elle donne le sens des anciennes figures Chinoises de Fohi (Explicação da aritmética binária, que se serve apenas dos caracteres 0 e 1, com observações sobre sua utilidade e sobre o sentido que dá às antigas figuras chinesas de Fuxi). Esse texto pode ser lido na página https://fredlopes.com.br/matematica/historia-da-matematica/
Nesse artigo, Leibniz mostra como codificar todos os números através de um sistema de numeração de base 2 que necessita apenas de dois símbolos, 0 e 1. Além disso, e porque recebeu de um amigo uma cópia do I Ching , Leibniz percebeu as ligações entre os trigramas do livro e o seu sistema, vislumbrando, assim, mais um passo na construção da sua língua universal, chamado por ele de characteristica universalis.
Vamos a um exemplo. Tome a sequência geométrica 1, 2, 4, 8, 16, 32… em que cada número é o dobro do número anterior. Leibniz percebeu que qualquer número inteiro pode ser escrito como a soma de alguns números dessa série. Por exemplo, 51 pode ser escrito como 32 + 16 + 2 + 1, começando do maior número para o menor. Observe que você não usou os números 8 e 4. Assim, se você fixar a série como 32, 16, 8, 4, 2, 1 e “marcar” com 1 aqueles números que foram utilizados e com 0 aqueles que não o foram, temos a sequência 1, 1, 0, 0, 1, 1, indicando que usei 32, usei 16, não usei 8, não usei 4, usei 2 e usei 1. Escrevendo sem as vírgulas, temos o número 110011, que lemos um, um, zero, zero, um, um .
O artigo vai além e indica como somar, subtrair, multiplicar e dividir esses números binários. O que Leibniz não imaginou é que esse sistema de numeração viria a ser utilizado 250 anos depois no desenvolvimento dos modernos computadores – do celular que você usa para ler este texto.
Discussão
Leibniz foi outro filósofo que se dedicou muito à matemática. Por que será que boa parte dos filósofos ocidentais foram também matemáticos ou, pelo menos, ensinaram matemática em algum momento de suas vidas? Pense também no seguinte:
1. Você acha que as operações aritméticas devem ser ensinadas nas escolas apenas para que possamos operar computadores com segurança? Se uma máquina calcula melhor do que nós, por que precisamos aprender, por exemplo, a dividir dois números longos?
2. O princípio dos indiscerníveis de Leibniz é um princípio lógico definitivo e universal? Você concorda com ele?
3. Você acredita na possibilidade de criação de uma língua universal a ser utilizada na comunicação humana?
4. A numeração binária de Leibniz foi utilizada pelo matemático inglês George Boole (1815 – 1864) na algebrização da lógica, algebrização que foi utilizada pelos pioneiros da computação digital. Você acha que esse é um exemplo de como o conhecimento desinteressado e a pesquisa básica sem pretensões utilitárias devem ser mantidos e custeados com dinheiro público?
Bibliografia
AABOE, A. Episódios da História Antiga da Matemática . Rio de Janeiro: SBM, 1984.
BOYER, C. B. História da Matemática . São Paulo, Edgard Blucher, 1974.
DAVIS, Philip J.; HERSH, Reuben. A experiência matemática . Lisboa: Gradiva, 1995.
EVES, H. Introdução à História da Matemática . Campinas, Ed. da Unicamp, 1995.
IFRAH, Georges. Números: a história de uma grande invenção . Rio de Janeiro: Globo, 1998.
KATZ, Victor. A History of Mathematics . New York: HarperCollins, 1993.
PICKOVER, Clifford. The Math Book . New York: Sterling, 2009.
STRUIK, Dirk J. História concisa das Matemáticas . Gradiva, Lisboa, 1992.
Na internet, a Wikipedia (preferencialmente em inglês) é, de longe, o melhor site para mais informações sobre os tópicos tratados aqui, assim como o Wolfram Alpha .